Modelización estadística de la población para apoyar los censos

class: center, middle, inverse, title-slide

# Modelización estadística de la población para apoyar los censos
## Día 1
### Edith Darin

---

<div>
<style type="text/css">.xaringan-extra-logo {
width: 120px;
height: 148px;
z-index: 0;
background-image: url(../assets/pic/funders_logo.png);
background-size: contain;
background-repeat: no-repeat;
position: absolute;
bottom:-5.5em;left:1em;
}
.custom-slide-content {
	font-size: 1.9rem !important;
	font-weight: 600 !important;
	color: #ff8000 !important;
}
</style>
<script>(function () {
 let tries = 0
 function addLogo () {
 if (typeof slideshow === 'undefined') {
 tries += 1
 if (tries < 10) {
 setTimeout(addLogo, 100)
 }
 } else {
 document.querySelectorAll('.remark-slide-content:not(.title-slide):not(.inverse):not(.hide_logo)')
 .forEach(function (slide) {
 const logo = document.createElement('div')
 logo.classList = 'xaringan-extra-logo'
 logo.href = null
 slide.appendChild(logo)
 })
 }
 }
 document.addEventListener('DOMContentLoaded', addLogo)
})()</script>
</div>

# Agenda del día

--

### 1. Introducción global a la modelización de la población

--

### 2. Presentación del tutorial 1: ¿cómo pensar en la población como un bayesiano?

---
class: bottom, hide_logo

# Esquema de la presentación

--

### 1. Modelos de población en WorldPop

### 2. Por qué bayesiano

--
### 3. Fundamentos bayesianos

--
### 4. Estimación bayesiana de modelos

--
### 5. Esquema del curso

--
### 6. Material didáctico

---
class: inverse, left, middle

# Modelos de población en WorldPop

---
class: center, middle

# Objetivo

---
class: left, middle
background-image: url(day1_presentation_files/pic/background_griddedpop.png)

## .bg-white[Estimación de la población local]

---
class: hide_logo

# Cuadrícula de población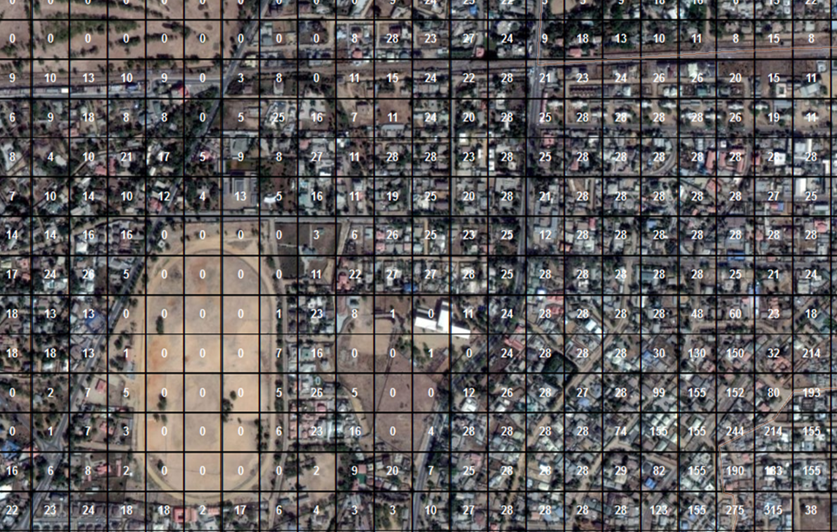

![](day1_presentation_files/pic/griddedpop_ex.png)

---

# Ventajas de la cuadrícula de población

.pull-left[
### 1. Descripción de las variaciones espaciales finas
]

.pull-right[
![](day1_presentation_files/pic/griddedpop_zoom.png)
]
---
# Ventajas de la cuadrícula de población

.pull-left[

### 2. Formato coherente y comparable
-    Tamaño idéntico
-    Forma idéntica
-    Constante en el tiempo
]

.pull-right[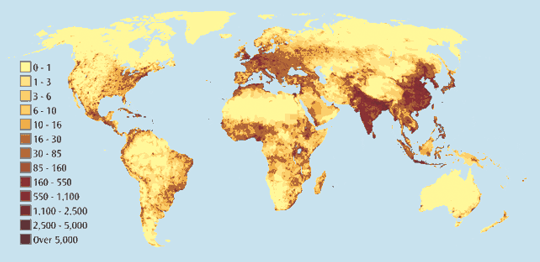
![](day1_presentation_files/pic/gridcell_world.png)

![](day1_presentation_files/pic/gridcell.png)
]

---

# Ventajas de la cuadrícula de población

.pull-left[
### 3. Agregación espacial personalizada

- Alrededor de un punto*: centro de salud, escuela, centro de terremotos*

- Alrededor de una línea*: río, bordes de carreteras*

- En una zona*: pueblos, cuenca hidrográfica*
]

--
.pull-right[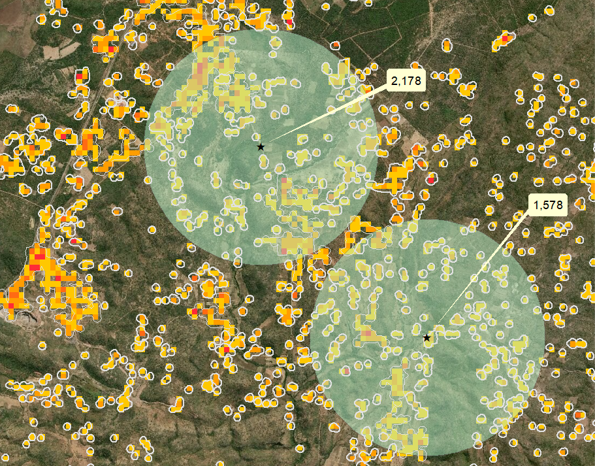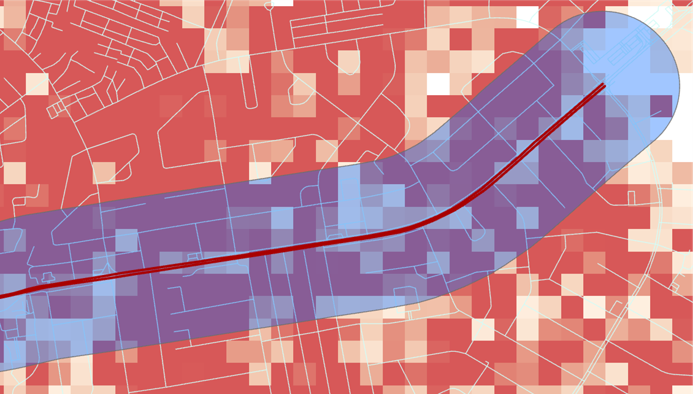
![](day1_presentation_files/pic/griddedpop_agreg_pts.png)
![](day1_presentation_files/pic/griddedpop_agreg.png)
]

---

# Ventajas de la cuadrícula de población

.pull-left[
### 4. Combinación flexible de datos

]

.pull-right[
![](day1_presentation_files/pic/griddedpop_use.png)

]

---
class: left, middle
background-image: url(day1_presentation_files/pic/background_griddedpop.png)

## .bg-white[Dos tipos de modelo]

---
class: inverse, center, middle

# Cuando se dispone de datos de población con cobertura **espacial completa**

---
class: center, middle

# Modelo descendente

---

# Modelo descendente

![](day1_presentation_files/pic/schema1. png.png)
---
# Tutorial R descendente

![](day1_presentation_files/pic/topdown_tuto.PNG)

https://htmlpreview.github.io/?https://github.com/wpgp/top-down-tutorial/blob/master/4_tutorial.html

---
class: inverse, center, middle

# Cuando **no se** dispone de datos de población con cobertura espacial completa

---
class: center, middle

![](day1_presentation_files/pic/issue_pop.png)

---

# Modelo ascendente

![](day1_presentation_files/pic/schema2.jpg)

---
# Modelos disponibles

![](day1_presentation_files/pic/current_pop.png)

.center[https://wopr.worldpop.org/?/Population]

---
class: left, middle
background-image: url(day1_presentation_files/pic/background_griddedpop.png)

## .bg-white[Característica común:  &nbsp; ]
## .bg-white[¡Todos son modelos bayesianos!  &nbsp;]

---

class:inverse, left, middle

# ¿Por qué la estadística bayesiana?

---
class: center, middle

# Pero ¿qué es la estadística bayesiana?

---
class: center, middle

### 1. La estadística bayesiana es un proceso de **construcción del conocimiento**
---
class: hide_logo

# Un ejemplo de la vida cotidiana

![](day1_presentation_files/pic/restaurant_diagram.png)

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

---
class: middle, hide_logo

.pull-left[
###Filosofía bayesiana: 
1. disponer de información a *priori* sobre un fenómeno
2. interpretar los datos entrantes a la luz de esta información a *priori*
3. concluir con información actualizada o a *posteriori*]

.pull-right[
![](day1_presentation_files/pic/bayes_diagram.png)
]

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

---
layout: true
class: hide_logo

# Pon a prueba tu pensamiento bayesiano

---

.center2[*Al lanzar una moneda al aire, decimos que “la probabilidad de que salga cara es de 0.5.’*

¿Cómo interpretas esta probabilidad?

1. Si lanzo esta moneda una y otra vez, aproximadamente el 50 % de las veces saldrá cara.
2. Cara y cruz son igualmente probables.]

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

---

.center2[*Se acercan unas elecciones y un encuestador afirma que “el candidato A tiene un 0,9 probabilidades de ganar.’*

¿Cómo interpretas esta probabilidad?

1. Si observamos las elecciones una y otra vez, el candidato A ganará aproximadamente el 90 % de las veces.
2. El candidato A tiene muchas más probabilidades de ganar que de perder.
3. El cálculo del encuestador es erróneo. El candidato A ganará o perderá, por lo que su probabilidad de ganar solo puede ser 0 o 1.]

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

---
.center2[*Consideremos dos afirmaciones:*

*(1) Zuofu afirma que puede predecir el resultado del lanzamiento de una moneda. 
Para probar su afirmación, lanzas una moneda al aire 10 veces y él predice correctamente las 10.*

*(2) Kavya afirma que puede distinguir los edulcorantes naturales de los artificiales. 
Para probar su afirmación, le ofreces 10 muestras de edulcorantes y ella identifica correctamente cada uno de ellos*

¿Cuál es tu conclusión?

1. Confías más en la afirmación de Kavya que en la de Zuofu.
2. La evidencia que apoya la afirmación de Zuofu es tan fuerte como la evidencia que apoya la afirmación de Kavya.]

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

---
layout:false
class: center, middle

### 2.  La estadística bayesiana es una **perspectiva** diferente **de la probabilidad**
---
class: hide_logo, middle
# Definir la probabilidad

.footnote[[Capítulo 1, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-1.html)]

> ### **Filosofía bayesiana**: la *probabilidad* mide la verosimilitud *relativa* de un acontecimiento.

--
> ### **Filosofía frecuentista**: la probabilidad mide la *frecuencia relativa a largo* plazo de un acontecimiento *repetible*.

---
class: center, middle

### 3.  La estadística bayesiana es **transparente en cuanto a las hipótesis realizadas**

---
# Teorema de Bayes

$$ \text{posterior} \quad = \quad \frac{\text{prior } \cdot \text{ likelihood}}{\text{normalizing constant}} \; $$

**Modelo de probabilidad a priori** 
Refleja nuestra creencia sobre el fenómeno antes de ver cualquier dato.

**Probabilidad** 
Representa el rango de valores de los parámetros acompañado de la probabilidad de que cada parámetro explique los datos que observamos.

**Modelo de probabilidad a posteriori** 
Resume la verosimilitud de un fenómeno.

---
# Ejemplo ficticio

#### Pregunta del modelador: *¿Lloverá mañana, 27 de septiembre de 2021, en el Reino Unido?*

--

**Modelo de probabilidad a priori**: 
En septiembre llueve el 60 % del tiempo en el Reino Unido.

**Probabilidad** 
Hoy hay sol y los modelos climáticos dicen que el tiempo es estable en un 40 % de los casos.

**Modelo de probabilidad a posteriori** 
Conociendo el tiempo de hoy en el Reino Unido y los modelos climáticos, podemos actualizar la información a priori del tiempo para el 27 de septiembre en el Reino Unido.

---
# Equilibrio entre los datos y el conocimiento

![](day1_presentation_files/pic/bayes-balance-1.png)

--
A medida que recopilamos más datos, los datos previos pierden su influencia.

.footnote[Más detalles en [ el capítulo 2, Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/chapter-2.html)
]
---

class: center, middle

### 4.  La estadística bayesiana tiene en cuenta la **incertidumbre del modelo**
---
# Cuantificación de la incertidumbre

### Fuentes de incertidumbre 
- Indicadores faltantes
--

- Errores en la recolección de datos
--

- Representatividad imperfecta de la muestra
--

- Variación individual

--

#### **Los parámetros se consideran variables y, por lo tanto, tienen una distribución**

--
#### **Las predicciones se consideran variables y, por lo tanto, tienen una distribución**

---
class: center, middle

### 5.  Los modelos bayesianos te hacen pensar en tu pregunta en términos de **distribuciones**

---
class: center, middle

#¿Por qué la estadística bayesiana?

--
### Basada en principios

### Flexible

### Adecuada para datos faltantes

### Simple

---
class: inverse, middle, center

# Estimación de modelos bayesianos
---
.custom-slide-content[Método de Monte Carlo basado en cadenas de Markov]

#### **Objetivo**: Aproximación de la distribución a posteriori mediante simulación
--

**Monte Carlo** 
Estimación de un parámetro generando números aleatorios y comprobando si se corresponde con la estructura

--
.pull-right[
![](day1_presentation_files/pic/monte_carlo.png)
]

---
.custom-slide-content[Método de Monte Carlo basado en cadenas de Markov]

#### **Objetivo**: Aproximación de la distribución a posteriori mediante simulación

**Monte Carlo** 
Estimación de un parámetro generando números aleatorios y comprobando si se corresponde con la estructura

**Cadena de Markov** 
Secuencias de muestras relacionadas probabilísticamente

---
.custom-slide-content[Método de Monte Carlo basado en cadenas de Markov]

#### **Objetivo**: Aproximación de la distribución a posteriori mediante simulación

**MCMC** 
1. Elige un valor de parámetro aleatorio
2. Evalúa la probabilidad de que el valor explique los datos teniendo en cuenta la creencia a priori y el modelo
3. Dibuja otro valor en función de la bondad del valor anterior

--
.pull-right[
![](day1_presentation_files/pic/mcmc.png)
]

[Introducción de cero matemáticas a los métodos MCMC](https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50)

---
# Stan

[Stan](http://mc-stan.org/) es un lenguaje de programación probabilístico para la estimación bayesiana

Modo administrador independiente del idioma y la plataforma con una **amplia gama de interfaces de usuario**:
- Shell (“CmdStan”)
- **R (“RStan”) **
- Python (“PyStan”) 
- Matlab (“MatlabStan”)
- Stata (“StataStan”)
- Julia (“JuliaStan”)

Proceso de compilación en dos pasos: modelo en código `stan`, traducido a `C++` y compilado en un binario independiente

.footnote[Equipo de desarrollo de Stan. 2021. Guía del usuario y manual de referencia del lenguaje de modelización Stan, 2.27. https://mc-stan.org
]
---
class: inverse, middle, center

# Lecturas complementarias
---

# Lecturas complementarias

1. [Bayes Rules! An Introduction to Bayesian Modeling with R ](https://www.bayesrulesbook.com/)
by Alicia A. Johnson, Miles Ott, Mine Dogucu

2. [An Introduction to Bayesian Data Analysis for Cognitive Science](https://vasishth.github.io/bayescogsci/book/)
by Bruno Nicenboim, Daniel Schad, and Shravan Vasishth

3. [Bayesian Data Analysis](http://www.stat.columbia.edu/~gelman/book/BDA3.pdf), by Andrew Gelman, John Carlin, Hal Stern,
Donald Rubin, David Dunson, and Aki Vehtari

4. [Bayesian Data Analysis course](https://avehtari.github.io/BDA_course_Aalto/), by Aki Vehtari

5. [Bayesian workflow](http://www.stat.columbia.edu/~gelman/research/unpublished/Bayesian_Workflow_article.pdf), by Andrew Gelman et al

---
class: inverse, middle, center

# Esquema del curso
---

## Tutorial 1: Cómo pensar en la población como un bayesiano

#### Modelo normal con datos simulados
--

#### Modelo de Poisson con datos reales

.center[![](day1_presentation_files/pic/model_l1.PNG)]

#### Modelo lognormal con datos reales
.center[![](day1_presentation_files/pic/model_l2.PNG)]
---

## Tutorial 2: ¿Cómo modelizar las variaciones espaciales a gran escala?

#### Modelo jerárquico con datos reales
.center[![](day1_presentation_files/pic/model_l3.PNG)]

---

## Tutorial 3: ¿Cómo modelizar las variaciones espaciales a pequeña escala?

#### Modelo de covariables con datos reales

.center[![](day1_presentation_files/pic/model_l4.PNG)]
---
## Tutorial 4: Diagnóstico y predicción avanzados de modelos

---

# Material didáctico

- Toda la presentación del curso y el tutorial están disponibles en este sitio web:
https://wpgp.github.io/bottom-up-tutorial/

- El código en bruto puede encontrarse en Github: 
https://github.com/wpgp/bottom-up-tutorial

- Flujo de trabajo del taller:
--

-   Tutoriales guiados con presentación y revisión en directo
--

- Entre sesiones: GitHub Issues o correo electrónico: e.c.darin@soton.ac.uk
--

- Taller de coconstrucción: **¡No dudes en hacernos llegar tus comentarios sobre el contenido!**